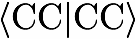
CFOUR | Main / Additional Keywords For Excited State-calculations

The following keywords can be used to control an excited-state calculation:

CIS_CONV:

specifies the convergence threshold (as 10^N with N as the value specified) used in the solution of the CIS eigenvalue problem (default is 5).

ESTATE_TOL (to be replaced in the next release by ESTATE_CONV):

specifies the convergence threshold used in solving the right- and/or left-handside eigenvalue porblem in CC-LR/EOM-CC calculations. The iterative diagonalization is continued until the RMS residual falls below 10^{-N} with N as the value specified with this keyword (default is 5).

ESTATE_MAXCYC:

specifies the maximum number of iterations used in the solution of the EOM-CC/CC-LR equations (default is 20).

ESTATE_PROP:

needs to be set to EXPECTATION in order to obtain transition moments. Note that this option is only available for CCSD and that a request for the calculation of transition moments approximately doubles the computational costs. Furthermore, the keyword ESTATE_PROP should not be used in analytic gradient calculations.

Concerning the Zeta equations which need to be solved in EOM-CCSD/CCSD-LR analytic gradient calculations, the same keywords as for the Lambda equations are to be used, i.e. LINEQ_TYPE, LINEQ_CONV, and LINEQ_MAXCYC.

EOM_NSTATES:

for experimental use only. Selects the iterative diagonalization algorithm for the EOMEE calculations. If set to DAVIDSON, the general modified Davidson technique is used. If set to MULTIROOT, a multi-root Davidson approach is invoked that evaluates all roots of a symmetry block simultaneously. This approach is much more stable if the roots are energetically close to each other.

EOM_PROPSTA:

selects the excited state the EOMEE properties are calculated for. Only valid if EOM_NSTATES = MULTIROOT is set. It always refers to the corresponding state of the last symmetry block considered. If not set, the properties are calculated for the last excited state.