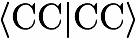I. Electronically excited states
a) configuration interaction singles (CIS) approaches
CIS, also known as Tamm-Dancoff approximation (TDA))
I. Tamm, J. Phys. USSR 9, 449 (1945)
S.M. Dancoff, Non-adiabatic meson theory of nuclear forces, Phys. Rev. 78, 382 (1950)
J.B. Foresman, M. Head-Gordon, J.A. Pople, and M.J. Frisch, Toward a systematic molecular orbital theory for excited states, J. Phys. Chem. 96, 135-149 (1992)
CIS plus a perturbative corrections for doubles (CIS(D))
M. Head-Gordon, R.J. Rico, M. Oumi, and T.J. Lee, A doubles correction to electronic excited states from configuration interaction in the space of single substitutions, Chem. Phys. Letters 219, 21-29 (1994)
CIS(D) gradients
J.F. Stanton, J. Gauss, N. Ishikawa, and M. Head-Gordon, A comparison of single reference methods for characterizing stationary points of excited state potential energy surfaces, J. Chem. Phys. 103, 4160 (1995)
b) via coupled-cluster linear response (CC_LR) theory
review on CC response theory
O. Christiansen, C. Hättig, and P. Jørgensen, Response functions from Fourier component variational perturbation theory applied to a time‐averaged quasienergy, Int. J. Quantum Chem. 68, 1-52 (1998)
CC linear response theory
H.J. Monkhorst, Calculation of properties with the coupled‐cluster method, Int. J. Quant. Chem. Symp. 11, 421-432 (1977)
H. Koch and P. Jørgensen, Coupled cluster response functions, J. Chem. Phys. 93, 3333 (1990)
CCSD-LR
H. Koch, H.J.Aa. Jensen, P. Jørgensen and T. Helgaker, Excitation energies from the coupled cluster singles and doubles linear response function (CCSDLR). Applications to Be, CH+, CO, and H2O, J. Chem. Phys. 93, 3345 (1990)
CC3-LR
O. Christiansen, H. Koch, and P. Jørgensen, Response functions in the CC3 iterative triple excitation model, J. Chem. Phys. 103, 7429 (1995)
CC-LR for general CC models
M. Kállay and J. Gauss, Calculation of excited-state properties using general coupled-cluster and configuration-interaction models, J. Chem. Phys. 121, 9257 (2004)
CC-LR for Mk-MRCC theory
T.-C. Jagau and J. Gauss, Linear-response theory for Mukherjee's multireference coupled-cluster method: Excitation energies, J. Chem. Phys. 137, 044116 (2012)
c) via an equation-of-motion coupled-cluster (EOM-CC) ansatz
EOM-CCSD
J.F. Stanton and R.J. Bartlett, The equation of motion coupled‐cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties, J. Chem. Phys. 98, 7029 (1993)
EOM-CCSDT
K. Kowalski and P. Piecuch, The active-space equation-of-motion coupled-cluster methods for excited electronic states: Full EOMCCSDt, J. Chem. Phys. 115, 643 (2001)
S.A. Kucharski, M. Wloch, M. Musial, and R.J. Bartlett, Coupled-cluster theory for excited electronic states: The full equation-of-motion coupled-cluster single, double, and triple excitation method, J. Chem. Phys. 115, 8263 (2001)
Y. Bomble, K.W. Sattelmeyer, J.F. Stanton, and J. Gauss, On the vertical excitation energy of cyclopentadiene, J. Chem. Phys. 121, 5236 (2004); present implementation within Cfour
EOM for general CC models
M. Kállay and J. Gauss, Calculation of excited-state properties using general coupled-cluster and configuration-interaction models, J. Chem. Phys. 121, 9257 (2004)
c) property calculations in CC-LR/EOM-CC
analytic gradients for EOM-CCSD/CCSD-LR
J.F. Stanton, Many‐body methods for excited state potential energy surfaces. I. General theory of energy gradients for the equation‐of‐motion coupled‐cluster method, J. Chem. Phys. 99, 8840 (1993) (theory)
J.F. Stanton and J. Gauss, Analytic energy gradients for the equation‐of‐motion coupled‐cluster method: Implementation and application to the HCN/HNC system, J. Chem. Phys. 100, 4695 (1994) (implementation)
J.F. Stanton and J. Gauss, Analytic energy derivatives for the equation-of-motion coupled-cluster method: Algebraic expressions, implementation and application to theS 1 state of HFCO, Theor. Chim. Acta 91, 267-289 (1995) (implementation)
analytic gradients for general EOM-CC/CC-LR
M. Kállay and J. Gauss, Calculation of excited-state properties using general coupled-cluster and configuration-interaction models, J. Chem. Phys. 121, 9257 (2004)
II. Ionized states
EOMIP-CCSD
J.F. Stanton and J. Gauss, Analytic energy derivatives for ionized states described by the equation‐of‐motion coupled cluster method, J. Chem. Phys. 101, 8938 (1994)
EOMIP-CC3 and EOMIP-CCSDT-n
J.F. Stanton and J. Gauss, A simple scheme for the direct calculation of ionization potentials with coupled-cluster theory that exploits established excitation energy methods, J. Chem. Phys. 111, 8785 (1999)
EOMIP-CCSD(2)
J.F. Stanton and J. Gauss, Perturbative treatment of the similarity transformed Hamiltonian in equation‐of‐motion coupled‐cluster approximations, J. Chem. Phys.103, 1064 (1995)
analytic gradients for EOMIP-CCSD
J.F. Stanton and J. Gauss, Analytic energy derivatives for ionized states described by the equation‐of‐motion coupled cluster method, J. Chem. Phys. 101, 8938 (1994)
III. Electron-attached states
EOMEA-CCSD
M. Nooijen and R.J. Bartlett, Equation of motion coupled cluster method for electron attachment, J. Chem. Phys. 102, 3629 (1996)
analytic gradients for EOMEA-CCSD
J.F. Stanton and J. Gauss, unpublished
IV. Finite Magnet-Field Methods
F. Hampe and S. Stopkowicz, Equation-of-motion coupled-cluster methods for atoms and molecules in strong magnetic fields, J. Chem. Phys. 146, 154105 (2017)
F. Hampe and S. Stopkowicz, Transition-dipole moments for electronic excitations in strong magnetic fields using equation-of-motion and linear response coupled-cluster theory, J. Chem. Phys. 15, 4036 (2019)
M.-P. Kitsaras and S. Stopkowicz, The approximate coupled-cluster methods CC2 and CC3 in a finite magnetic field, J. Chem. Phys. 160, 094112 (2024)