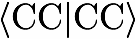
CFOUR | Main / Finite-nucleus Model For Relativistic Calculations

For relativistic calculations it is in particular for heavy-element compounds important to account for the finite size of the nuclei. This is usually done by using a specific model for the nuclear charge distribution and to use this model to evaluate the corresponding nuclear attraction integrals. Most popular in this context are Gaussian charge distributions, as they are rather easily implemented using standard Gaussian integral codes. Those models are based on the following formula for the charge distribution

{$ \rho^{G}(R)=\rho_0^{G} \exp(- \zeta R^2) $}

with

{$ \rho_{0}^{G} = eZ ( \frac{\zeta}{\pi} )^{\frac{3}{2}} $}

and

{$ \zeta = 3/ (2 <R^2>) $}

The root mean square radii of the nucleus is related to the mass number A (note that CFour assumes here the most abundant isotope) via the following empirical expression

{$ \sqrt{<R^2>} = 0.836 A^{1/3} + 0.570 fm $}

(for further information and references, see http://dirac.chem.sdu.dk/doc/FiniteNuclei/FiniteNuclei.shtml

Note that this feature is not part of the public release.