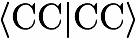Population analysis
Mulliken population analysis
R.S. Mulliken, Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I, J. Chem. Phys. 23, 1833 (1955)
HF stability analysis
J. Paldus and J. Čížek, Stability Conditions for the Solutions of the Hartree–Fock Equations for Atomic and Molecular Systems. II. Simple Open‐Shell Case, J. Chem. Phys. 52, 2919 (1970)
R. Seeger and J.A. Pople, Self‐consistent molecular orbital methods. XVIII. Constraints and stability in Hartree–Fock theory, J. Chem. Phys. 66, 3045 (1977)
T.D. Crawford, J.F. Stanton, W.D. Allen, and H.F. Schaefer III, Hartree–Fock orbital instability envelopes in highly correlated single-reference wave functions, J. Chem. Phys. 107, 10626 (1997)
Effective-Core Potentials
L.R. Kahn, P. Baybutt, and D.G. Truhlar, Ab initio effective core potentials: Reduction of all‐electron molecular structure calculations to calculations involving only valence electrons, J. Chem. Phys. 65, 3826 (1976)
A.V. Mitin and C. van Wüllen, Two-component relativistic density-functional calculations of the dimers of the halogens from bromine through element 117 using effective core potential and all-electron methods, J. Chem. Phys. 124, 064305 (2006); implementation used within CFour
Local correlation methods
definition of localized orbitals
P. Pipek and P.G. Mezey, A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions, J. Chem. Phys. 90, 4916 (1989); available within CFour
C. Edminston and K. Ruedenberg, Localized Atomic and Molecular Orbitals, Rev. Mod. Phys. 35, 457 (1963)
F. Boys, Construction of Some Molecular Orbitals to Be Approximately Invariant for Changes from One Molecule to Another, Rev. Mod. Phys. 32, 296 (1960); J.M. Foster and F. Boys Canonical Configurational Interaction Procedure, Rev. Mod. Phys. 32, 300 (1960); available within CFour
general concepts
S. Sæbo and P. Pulay, Local treatment of electron correlation, Ann. Rev. Phys. Chem. 44, 213-236 (1993); review
local MP2
local MP2 gradients
A. El Azhary, G. Rauhut, P. Pulay, and H.-J. Werner, Analytical energy gradients for local second-order Møller–Plesset perturbation theory J. Chem. Phys. 108, 5185 (1998); implementation within MOLPRO
local MP2 polarizabilities and NMR chemical shifts
J. Gauss and H.-J. Werner, NMR chemical shift calculations within local correlation methods: the GIAO-LMP2 approach, Phys. Chem. Chem. Phys. 2, 2083-2090 (2000); pilot implementation
Basis-Set Superposition Error
definition
B. Liu and A.D. McLean, Accurate calculation of the attractive interaction of two ground state helium atoms, J. Chem. Phys. 59, 4557 (1973)
counterpoise correction
S.F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys. 19, 553-566 (1970)
Finite Magnet-Field Methods
S. Stopkowicz, J. Gauss, K.K. Lange, E.I. Tellgren and T. Helgaker, Coupled-cluster theory for atoms and molecules in strong magnetic fields, J. Chem. Phys. 143, 074110 (2015)
F. Hampe and S. Stopkowicz, Equation-of-motion coupled-cluster methods for atoms and molecules in strong magnetic fields, J. Chem. Phys. 146, 154105 (2017)
F. Hampe, N. Gross, and S. Stopkowicz, Full triples contribution in coupled-cluster and equation-of-motion coupled-cluster methods for atoms and molecules in strong magnetic fields, Phys. Chem. Chem. Phys. 22, 23522 (2020)
M.-P. Kitsaras and S. Stopkowicz, The approximate coupled-cluster methods CC2 and CC3 in a finite magnetic field, J. Chem. Phys. 160, 094112 (2024)
CFOUR is partially supported by the U.S. National Science Foundation.