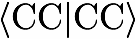
|
Main /
Theoretical Details To DBOC CorrectionsCorrections for making the Born-Oppenheimer approximations in the quantum chemical treatment of atoms and molecules are easily computed using perturbation theory. The lowest-order correction is obtained in first-order and takes the form {$\Delta E_{DBOC} = \langle \Psi_{el} | \sum_A - \frac{\hbar^2}{2 M_A} \nabla_A^2 | \Psi_{el}\rangle $} This correction is known as the "diabatic Born-Oppenheimer correction (DBOC)" and its inclusion leads to the so-called adiabatic approximation with mass-dependent potentials that are different for the various isotopomers of a molecule. As shown by Handy, Yamaguchi, and Schaefer (J. Chem. Phys. 84, 4481 (1986)), analytic derivative techniques can be used to compute E(DBOC). At the HF-SCF level, the DBOC correction can be thus calculated as {$\Delta E_{DBOC}^{HF} = - \sum_A \frac{\hbar^2}{2 M_A} \langle \Psi_{HF} | \nabla^2_A | \Psi_{HF} \rangle $} {$ = \sum_A \frac{\hbar^2}{2 M_A} \langle \nabla_A \Psi_{HF} | \nabla_A \Psi_{HF}\rangle $} {$ = \sum_A \frac{\hbar^2}{2 M_A} \sum_i \langle \nabla_A \varphi_i | \nabla_A \varphi_i\rangle - \sum_A \frac{\hbar^2}{2 M_A} \sum_{i,j} \langle \nabla_A \varphi_i | \varphi_j\rangle \langle \varphi_j|\nabla_A \varphi_i\rangle$} With the corresponding AO integrals and the CPHF coefficients {$U_{pq}^x$}, this can be recasted in the following form for RHF {$ \Delta E_{DBOC}^{HF} = \sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2M_A} \sum_{\mu, \nu} D_{\mu \nu} \langle \frac{\partial \chi_{\mu}}{\partial x_i} | \frac{\partial \chi_{\nu}}{\partial x_i}\rangle $} {$ + 4\sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2 M_A} \sum_i^{occ} \sum_r^{all} U_{ri}^{x_i} \langle r |\frac{\partial i}{\partial x_i}\rangle $} {$ + 4 \sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2 M_A} \sum_i^{occ} \sum_r^{all} (U_{ri}^{x_i})^2$} } {$ - 2 \sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2 M_A} \sum_i^{occ} \sum_j^{occ} (U_{ij}^{x_i} + \langle i|\frac{\partial j}{\partial x_i}\rangle)^2$} with {$D_{\mu \nu}$} as the RHF-SCF density matrix {$D_{\mu \nu} = \sum_i 2 c_{\mu i} c_{\nu i}$} For UHF, this yields {$ \Delta E_{DBOC}^{HF} = \sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2M_A} \sum_{\mu, \nu} D_{\mu \nu} \langle \frac{\partial \chi_{\mu}}{\partial x_i} | \frac{\partial \chi_{\nu}}{\partial x_i}\rangle $} {$ + 2 \sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2 M_A} \sum_i^{occ} \sum_r^{all} (U_{ri}^{x_i})^2$} } {$ - \sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2 M_A} \sum_i^{occ} \sum_j^{occ} (U_{ij}^{x_i} + \langle i|\frac{\partial j}{\partial x_i}\rangle)^2$} with {$D_{\mu \nu}$} as the UHF-SCF density matrix {$D_{\mu \nu} = \sum_i c_{\mu i} c_{\nu i}$} with the sum running over spatial orbitals instead of spin orbitals. A slightly different, though equivalent expression for the DBOC at the HF-SCF level has been given earlier by Handy et al (J. Chem. Phys. 84, 4481 (1986)). A corresponding scheme for correlated calculations of DBOC is currently implemented. {$ + 2\sum_A \sum_{x_i=x,y,z} \frac{\hbar^2}{2 M_A} \sum_i^{occ} \sum_r^{all} U_{ri}^{x_i} \langle r |\frac{\partial i}{\partial x_i}\rangle $} |