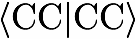
|
Main /
Theoretical Details To Partial AO AlgorithmsThe basic idea of partial AO algorithms is easily explained for the following term: {$Z_{ij}^{ab}=\sum_{e,f}\langle ab|ef\rangle t_{ij}^{ef}$} which is calculated as a) partial transformation of the amplitudes from MO to AO representation {$t_{ij}^{\mu \nu}=\sum_{e,f} c_{\mu e} c_{\nu f} t_{ij}^{ef}$} b) contraction with AO integrals {$Z_{ij}^{\mu \nu}=\sum_{\sigma \rho}\langle \mu \nu | \sigma \rho \rangle t_{ij}^{\sigma \rho}$} c) back transformation to the MO representation {$Z_{ij}^{ab}=\sum_{\mu,\nu}c_{\mu a}c_{\nu b}Z_{ij}^{\mu \nu}$} In this way, a full transformation of the AO two-electron integrals is avoided and the disk space requirements are drastically reduced. |