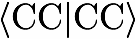
CFOUR | Main / Use Of Internal And Symmetry-adapted Internal Coordinates

[[Page link ?]]By default, force constants obtained in a vibrational frequency calculation are available in both the Cartesian representation and also in terms of the internal coordinates specified in the ZMAT file. On some occasions, it may be desirable to have force constants expressed in other ways, such as in symmetry coordinates. Because of the requirement that a "proper" ZMAT geometry specification must include symmetrically complete sets of internal coordinates, it is sometimes impossible to construct a ZMAT file with the same coordinates that you would like to use for calculating force constants. For example, most documented harmonic force fields for benzene include f_rr, where {r} is the C-C distance. It is not possible to make a ZMAT file that contains all six carbon-carbon distances, and one is usually forced to place one or two dummy atoms on the C₆ axis of the molecule. Clearly, there are not many people interested in force constants expressed in coordinate systems that include dummy atoms! Moreover, the out-of-plane force field of benzene usually is based on a peculiar kind of internal coordinate defined by the angle between a bond and the plane formed by two adjacent bonds. This is not one of the coordinates that can be used in a ZMAT file.

To facilitate comparisons of ab initio force constants with those in the literature, the user may specify an additional set or sets of coordinates. These will not be used in the course of the geometry optimization (those specified in the Z-matrix are always used), and are read only at the end of a vibrational frequency calculation. They are then used to construct matrices needed to transform first and second derivatives from the Cartesian representation to the coordinates that are specified.

The guidelines for defining alternative coordinate systems are as follows. If the coordinates of interest are simple internal coordinates (bond stretching, bond angle, dihedral angle or angle between a bond and a plane), then only one file is needed. This file is called INTCOORD and has the format described below:

Each internal coordinate is defined by two consecutive lines in the file. The first line contains a CHARACTER*1 variable that specifies the coordinate as an internuclear distance (R); the angle ABC defined by vectors from atom B to atom A and from atom B to atom C (A); the dihedral angle ABCD between the projections of the vectors CD and BA onto the plane perpendicular to the BC internuclear vector (D); and the angle between the plane formed by the BC and BD bonds and the bond between atoms A and B (W). The second line is an integer string and specifies the atoms involved in the particular coordinate. The numbering scheme for the atoms corresponds precisely to that in the ZMAT file, except that dummy atoms are not counted. Thus, atom number 6 is the sixth real atom that appears in the ZMAT file. For R, the two integers correspond to the atoms defining the distance; for angle ABC, the integers correspond to atoms A, B and C; for dihedral angle ABCD, the integers correspond to atoms A,B,C and D; and for the "Wilson" angle, the four atoms correspond to atoms C,D,A and B (the order is very important here!).

As an example, suppose the H₂O molecule is under study and the Z-matrix

X
O 1 RX
H 2 R 1 A
H 2 R 1 A 3 T

RX=1.0
RBH=1.3
A90=90.
T120=120.

is used, and it is desired to have force constants in terms of the internal coordinates defined by the two OH distances and the HOH angle. This would be specified by the following INTCOORD file:

R
1 2
R
1 3
A
2 1 3 0.52917708

This factor of 0.52917708 is necessary as a scaling factor and must be included after each angle. In many cases (notably, all molecules belonging to degenerate point groups), it is necessary to define somewhat more complicated coordinates that correspond to linear combination of some "primitive" set of internal coordinates. This may be done by use of an additional file called SYMCOORD, which has the following format:

Each composite coordinate is defined by three consecutive lines in the file. The first contains the number of primitive (i.e. internal) coordinates that contribute to the composite coordinate. The second contains a string of integers that defines which of the INTCOORD file coordinates are used; the indices correspond with the order of definition in the INTCOORD file. The third line specifies the coefficients that are attached to each primitive coordinate in the composite coordinate. These are automatically normalized by the program, so it is not possible to use unnormalized coordinates at the present time. An example which helps to clarify the SYMCOORD file protocol is given below, which defines the usual symmetry coordinates for water [S₁ = 2^-1/2 (r₁ + r₂ ); S₂ = θ; S₃ = 2^-1/2 (r₁ - r₂)]:

2
1 2
1. 1.
1
3
1.
2
1 2
1. -1.

After converting the force constants to the internal representation (followed by symmetry coordinates, specified either explicitly or constructed automatically), the harmonic problem is solved by the construction and diagonalization of the product of the G and F matrices, a procedure that is discussed in great detail in the class work of Wilson, Decius and Cross. If the calculation is run at a stationary point (as is presumably the usual case for you), the frequencies so obtained will agree exactly with those from the solution to the Cartesian problem (apart from "missing" rotations and translations); if the calculation is run at a non-stationary point, then the frequencies obtained by diagonalization of GF will agree precisely with the "rotationally" projected frequencies that appear just above the internal coordinate output.

A comment for internal coordinate aficionados:

If only the INTCOORD file is supplied, the program is capable of handling redundancies in the coordinate system. It uses the eigenvectors of the G matrix to construct as many sets of redundant combinations as is needed to generate an independent coordinate systems and then performs the required projection of the transformation matrices. The force constants are then reported in the INTCOORD file coordinates. An example of this, for the benzene molecule with the internal coordinate scheme used by Wilson, Decius and Cross in Chapter 10 of their book, can be found here.